CMR3 Reference Manual
Release Date 08/01/11
Copyright Notice
This document and the cmr and
xvpcmodels programs discussed herein are copyrighted
© 1992-2011 by Daylight Chemical Information Systems,
Inc. of Laguna Niguel, CA. Daylight explicitly grants
permission to reproduce this document under the condition
that it is reproduced in its entirety, including this
notice. All other rights are reserved. The underlying
program CMR3 is copyrighted (1988-2011) by Pomona
College and BioByte, Inc. of Claremont, CA. All rights are
reserved.
Table of Contents
1. Introduction2. Methods
3. Discussion
-
3.1 Single Bond Corrections to Atom Values
3.2 Correction for Multiple Bonds to Carbon
3.3 Higher Order Bonds between Hetero Atoms
3.4 Conjugation: Chain vs. Ring
3.5 Molar Refractivity of Solids
5. Appendix - Examples
1. Introduction
Molar Refractivity can be considered as the sum of either atom or bond refractivities. (1,2) This sum, which can be obtained directly from the compound's structure, should then equal the value given by the Lorenz-Lorenz equation when the measured values of density and refractive index have been inserted (3).
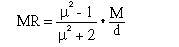
Historically the comparison of calculated with measured refractivities has made a significant contribution to the understanding of the nature of bonding electrons in organic molecules. Although M.R. has, to a great extent, been displaced from the frontier of structure determination by newer, more sophisticated techniques (NMR, GCMS, Fourier transform IR), it is now being looked upon with resurgent interest as a parameter for use in Quantitative Structure Activity Relationships (QSAR), especially in biological systems.(4) This renewed interest stems largely from the realization that, when care is taken in the design of a set of bioactive molecules so that covariance between M.R. and hydrophobicity is minimized, M.R. can serve as a measure of binding force between the polar portions of an enzyme and its substrate. Thus it was in-vivo binding and inhibition studies with purified enzymes which focused attention on the use of M.R. as a parameter in Biological QSAR. These initial encouraging results have since been confirmed as molecular models derived from X-ray crystallography indicate the correspondence of polar moieties in both enzyme and substrate at the active site.(5)
Even though the measurements necessary to obtain M.R. by the Lorenz-Lorenz equation are neither costly nor time-consuming, there are good reasons for calculating these values from structure. Obviously, calculation is the only alternative prior to synthesis, but even if the material is at hand, a considerable quantity of it is required to determine its density accurately. For solids, obtaining M.R. values via L-L presents numerous experimental difficulties.(6)
Although well suited to earlier users(e.g., structure verification), the methods of calculating M.R. from either bond or atom values were not ideal for use in QSAR. Some of these disadvantages are: (1) they require so many distinctions between closely related structural features that they are difficult to apply to the structures being considered by pesticide and medicinal chemists; (2) "fine-tuning" of values was performed with a simple analogous set with only that one feature, and much of this apparent precision is lost when such features are crowded together as they often are in commercially useful bioactive molecules; (3) reducing either method to an effective computer algorithm seemed impractical, and computer calculation of parameters is almost essential if QSAR specialists are to use them effectively.
2. Methods
The first task was to develop a "training set" of measured values; i.e. structures for which reliable index of refraction and density data were available. For this we relied heavily on the work of Vogel and his associates, published, to a large extent, in J. Chem. Soc. (7). Additional structural variety was added by means of data from International Critical tables(8) and Beilstein(9) (many of the latter accessed through Chemical Rubber Handbook). The Aldrich Chemical Catalog(10) proved to be a rich source, made the more reliable by the listing of percent purity (ordinarily a minimum of 97% was required for selection to the "training set"). Since Russian journals require index of refraction and density data when reporting the synthesis of a new organic compound, this turned out to be the best source for many unusual substructures appearing in the "training set". In all cases the index of refraction was measured at 20 C. If both were measured at the same temperature, values were acceptable between 15 C and 25 C. (M.R. is nearly temperature independent;see Discussion section following.) If the temperatures differed by no more than five degrees, the index of refraction was corrected by the coefficient of -0.0004/deg. Using these methods, a training set of nearly 1400 compounds was assembled to establish CMR. We anticipate doubling the size of this set before we attempt to develop improved versions.A modified linear regression analysis provided the basic framework for the search for a replacement for the atom-based(1) or bond-based (2) calculation procedures. Wiswesser Line Notation (WLN) served to encode each structure and as an identifier in the large tables of output. For computer analysis of structure, WLN was converted to SMILES. Other needed input was: molformula (from which the computer calculated molecular weight), index of refraction and density.
Using the L-L equation, the computer then calculated the observed M.R. which became the dependent variable in the regression equation. We then set out to investigate a series of independent Indicator Variables characteristic of the parts of each structure, the coefficients of which (in the regression equation) would be the numerical value of that part or feature, be it atom, bond or conjugation enhancement, etc.
Characterizing every bond type between all potential bonding pairs proved to be quite a formidable task, and would require a training set almost ten times as large as first assembled. And, of course, the use of simple atom values, ignoring bond types, supplied too little information. Before choosing some arbitrary compromise, we tried out the system which proved successful in calculating log P(o/w) from structure. This procedure defines polar fragments as those separated by "Isolating" (hydrogen-like) carbons. Using CLOGP fragments as Indicator Variables, an initial test set of 200 organic liquids of moderate structural variety was studied. The atom refractivity values for carbon and hydrogen which resulted were very close to those reported by Vogel(7). This was hardly surprising, since the polar fragments (OH, NH2, Cl, CONH2, etc.) contained all the bonds with the more mobile electrons, and the conjugation effect was contained in the specification of attachment (aliphatic, aromatic, vinyl, etc.).
As the training set was enlarged to provide greater structural variety, it became apparent that the unique specification of fragment types (so necessary in log P calculation) is not required for M.R. In fact, by carefully comparing the 95% confidence intervals for each variable as well as the overall regression coefficient and standard deviation, it was possible to "break down" each of the fragment types into its constituent atoms, as long as a few parameters for double bonds (i.e., C=O, C=S) were introduced. Contrary to expectation, no statistical justification was found for maintaining a distinction between aliphatic and aromatic attachment for heteroatoms or polar fragments. The distinction between the attachment of, say, a carbonyl fragment to a saturated vs. a conjugated hydrocarbon chain was significant, however. The significance of each of these simplifications is taken up in the following Discussion section.
The method which emerged as the result of this process of successive simplifications became the basis for CMR. It can be looked upon as an atom-based system augmented by corrections for a very few bond types: only five types of single bonds, eight types of double bonds, and few different degrees of conjugation.
IMPORTANT NOTE: In order to scale M.R. to bring it in line with the other parameters commonly used in QSAR, all values from the Lorenz-Lorenz equation have been multiplied by one-tenth(4).
3. Discussion
The advantages of using a global approach to calculating M.R., i.e., using the widest possible variety of structures in a single "training set", becomes obvious when one examines the need for distinguishing between primary, secondary and tertiary amines. The added precision resulting from this separation into three homologous series was evident to early workers in this field. Eisenlohr in 1912(11), Denbigh in 1940(12), Batsonov in 1961(13) and Miller in 1979(14) accepted the fact that, since it improves the calculation of the simpler structures, the separation is equally important for the more complex ones. Likewise, it was assumed that a separation between aliphatic and aromatic attached amine nitrogens was required for acceptable accuracy. It is instructive to examine, therefore, how much precision is lost using CMR in these situations, since CMR makes none of these distinctions.Table 1 lists the observed M.R. for a number of aliphatic and aromatic primary, secondary and tertiary amines, as well as for some amino-containing functional groups, such as hydrazines. The second column lists the M.R. from the L-L equation; the third column lists the deviation for the Vogel method of calculation, and the fourth the deviation for the CMR method.
| Compound | Molar Refractivity | Vogel Deviation | CMR Deviation |
| propyl amine | 1.9450 | .004 | .004 |
| i-butyl amine | 2.3984 | .000 | .007 |
| sec-butyl amine | 2.4100 | .000 | .000 |
| ethylenediamine | 1.8230 | .006 | .019 |
| aniline | 3.0560 | .017 | .003 |
| o-toluidine | 3.5369 | .000 | .020 |
| 2,3-dimethylaniline | 4.0080 | .006 | .027 |
| dimethylamine | 2.4218 | .002 | .017 |
| N-methyaniline | 3.5670 | .002 | .050 |
| N-ethylanliine | 4.0450 | .010 | .060 |
| triethylamine | 3.3790 | .015 | .046 |
| N,N-dimethylaniline | 4.0810 | .010 | .100 |
| N,N-dime-o-toluidine | 4.4603 | .095 | .010 |
| phenylhydrazine | 3.4062 | .065 | .012 |
| unsym-dime-hydrazine | 1.8689 | .020 | .020 |
| 1-me-1-phenylhydrazine | 3.9260 | .040 | .040 |
| Average | .0182 | .0272 |
Vogel's calculations require six structural parameters to account for the contribution to M.R. of an amine nitrogen while CMR only requires one. With six times the number of parameters, only a 50% improvement is noted in average deviation. CMR provides an even greater simplicity than is apparent from this table, for it uses the same nitrogen value when the nitrogen is bonded to F, Cl, Si, P, and As, as well as when it is triply-bonded in nitriles. Since the earlier procedures were never exhaustively reviewed and summarized, one could never be sure if an effect for one of these less common bonds had ever been determined.
3.1 Single Bond Correction to Atom Values
The assumptions implicit in an atom-based method are not all unreasonable if thought of in terms of that portion of the periodic table most pertinent to organic chemistry.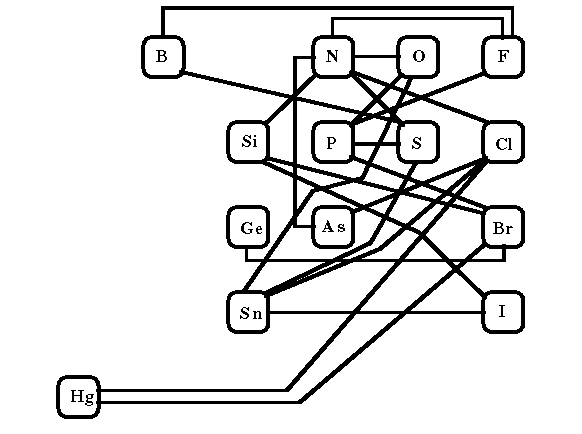
From Fig. 1, one sees that it is possible to include, within the atom
value, an average of all the variations possible for single bonds between
the elements separated by no more than three columns or rows. As Fig. 2
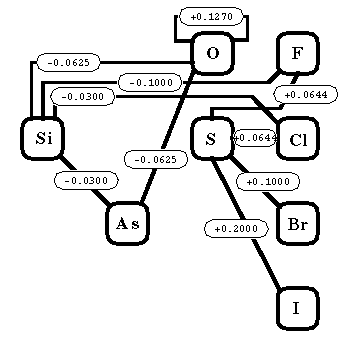
shows, the most common exceptions are the single bonds: Si-O, Si-F, As-O,
S-Cl and O-O, with the value for Si-Cl of marginal significance.
3.2 Correction for Multiple Bonds to Carbon
As expected, the refractivity of molecules containing double bonds is not the same as those with the same atoms singly bonded. When carbon is involved, refractivity is always increased by bonds of higher order, but with heteroatoms, the effect may be negative.The treatment of triple bonds by CMR may come as a surprise to chemists who ordinarily relate bond refractivity with bond order in the manner proposed by Denbigh(13). What is not immediately obvious from Denbigh's treatment is that NO exaltation is demonstrated when his relationship holds. Since the value per bond is constant (whether the bonds are counted in singles, doubles, or triples) the carbon ATOM value is also constant. It is not so strange, then, that CMR uses the same factor for an isolated double bond as for an isolated triple bond if the latter is in a ring or terminates a chain. Only when it is internal to a chain and/or conjugated with a polar double bond (e.g. a carbonyl) does the carbon-carbon triple bond have a higher refractivity than a double bond.
A carbon-nitrogen triple bond can be understood in much the same way. Ordinarily carbon and nitrogen atom values are sufficient for either aliphatic or aromatic nitriles. Only when conjugated with carbon-carbon double bonds in a chain is any exaltation seen for the nitrile, and this is taken care of by the values listed in Table 2. The carbon-nitrogen double bond fits into the same conceptual framework; i.e., no correction to atom values is necessary unless there is conjugation through the carbon valence, or if the nitrogen is attached to another hetero atom or polar fragment, such as carbonyl. The effect is additive if both conditions apply. This is more clearly apparent from Table 2 which appears at the end of Section 3.4.
3.3. Higher Order Bonds between Hetero Atoms
Before discussing the augmentation required by higher order bonds between hetero atoms, it is necessary to address the problems of representing and naming them. CMR uses the advanced SMILES utility which allows just four bond orders; single, double, triple and aromatic. (See SMILES section of this Manual). Bonds between nitrogen and oxygen of higher order than one are all treated as double. There is one such bond in nitroso compounds, amine oxides, and nitrites; in nitro compounds and nitrates there are two. It develops from regression analysis that the amount of bond augmentation to the atomic values is the same for one such bond in a nitroso fragment as for two such bonds in the nitro. This is supportive evidence that the two bonds are NOT of the same kind, even though, for simplicity, they are treated as equal.Sulfur-oxygen bonds are also treated as either single or double; there being one such double bond in a sulfoxide and two in a sulfone, sulfonamine or sulfonyl halide. In contrast to the case of the higher order N=O bonds, the bond augmentation for S=O bonds IS additive but NEGATIVE in sign. The sulfur-nitrogen double bond, S=N, appears only 15 times in the training set of 1362 compounds, and so its value of 0.19 is not very precise, but it does fit the following observation: The value for a double bond between sulfur and an atom in the row above it in the periodic table is negative for the atom in the same column (O), and increasingly more positive as one moves left to other atoms in this row (N,C).
The higher order bonds between phosphorus and elements in the next column right are also considered as double. The bond with oxygen (P=O), is highly negative (-.31), with the negativity decreasing down column VI (S=-.18;Se=-.12).
3.4 Conjugation: Chain vs. Ring
A surprising development arising from this method of evaluating refractivity factors is that conjugation within rings has an almost negligible effect, while in chains it is strongly positive. The calculation of M.R. for benzene yields essentially the same value whether the atom values are augmented by six aromatic bonds or by three isolated double bond values.Heteroatoms in aromatic rings are assigned two bonds by SMILES. Since hydrocarbon rings establish a rather high value for this bond, CMR would overpredict heteroaromatic rings unless a negative correction factor is assigned to heteroatoms in this context. A reasonably good approximation of this effect assigns a value of -.116 to both nitrogen and oxygen in heterocyles, with a 50% increase given for each lower row in the periodic table.
The most popular double bonds are "terminal"; i.e., they are not internal to a chain. Their values are given in Table 3. The enhancement by conjugation of these polar double bond with "internal" unsaturations and the enhancement of "internal" unsaturations with themselves is given in Table 2 at the end of this section.
To evaluate the entire spectrum of conjugation enhancement on "internal" unsaturations, a number of approaches were explored, but at present the only one which appears to offer reasonable precision combined with ease of computerization is the one summarized in Table 2. It operates with the following assumptions:
- The "base value" for an isolated unsaturation has been determined as 0.15, and the different ways this isolation can be lost can be assigned multiples of this "base" as 1.5X,2.0X,2.5X, and 3.0X respectively.>
- The carbon-carbon triple bond is considered "isolated" only if it is the terminal bond of a chain.>
- Either or both sides of the unsaturation under consideration can lose "isolation" through conjugation with either a "weakly polar" fragment (vinyl or phenyl, and indicated as "-") or a "strongly polar" one (e.g., carbonyl or sulfonyl, and indicated as "+"). All combinations of these effects must be allowed for. Note that a combination of "-" with "+" produces the maximum enhancement.>
| (As multiples of isolated of isolated unsaturation (+0.15)) | Neither X or Y Conjugated | Conjugated through Y | Conjugated through both X and Y |
| - + | -- ++ +- | ||
| Y-C=C-X chain ring | |||
| 1.0 | 1.5 1.5 | 2.0 2.0 3.0 | |
| 1.0 | 1.0 1.5 | 1.0 -- -- | |
| Y-C#C-X X = H interior | |||
| 1.0 | 1.5 1.5 | NA NA NA | |
| 1.5 | 1.5 2.0 | 2.0 2.0 2.0 | |
| Y-N=N-X | 1.0 | 1.5 -- | 3.0 -- -- |
| Y-C=NX X = C X = Si, O N, Cl C=O | |||
| 0.0 | 1.0 1.0 | NA NA NA | |
| 1.0 | 2.0 2.0 | -- -- -- |
| H = 0.0887 | Fe = 0.4400 |
| B = 0.3442 | Ge = 0.9536 |
| C = 0.2864 | As = 1.1750 |
| N = 0.2800 | Se = 1.1059 |
| O = 0.1531 | Br = 0.8657 |
| F = 0.1042 | Cd = 1.3304 |
| Si = 0.7087 | Sn = 1.4355 |
| P = 0.8569 | Te = 1.4770 |
| S = 0.8063 | I = 1.3951 |
| Cl = 0.5801 | Hg = 1.3129 |
| Ti = 1.6900 | Pb = 1.9185 |
| N = -0.1160 | Se = -0.1740 |
| O = -0.1160 | Te = -0.2600 |
| S -0.1740 |
| O-O = 0.1270 | Si-F = -0.1000 |
| O-Si =-0.0625 | Si-Cl = -0.0300 |
| O-As = -0.0625 | Si-As =-0.0300 |
| S-F = 0.0644a | S-Br = 1.0000 |
| S-Cl = 0.0644 | S-I = 2.0000 |
| C=O = + 0.060 | P=O = -0.308 |
| C=S = + 0.263 | P=S = -0.185 |
| N=O = + 0.114 | P=Se = -0.123 |
| N=S = + 0.186 | S=O = -0.120 |
3.5 Molar Refractivity of Solids
In many early studies the molar refractivities of solids were determined by measuring the refractive index of solutions in inert solvents and extrapolation to 100% solute.(15) Schuyler et.a.(6) clearly state the serious experimental and theoretical difficulties of this method. To include enough solids in the training set to establish whether or not CMR could be applied to them it was necessary to use density and refractive index data from the supercooled liquid or the melt at high temperatures.We could find five aliphatic hydrocarbons with density and index of refraction data taken at both 20 C and at 50-80 C higher. From this data it was found that the temperature coefficient of M.R. could be taken as +0.000617 per degree. Using this coefficient, 90 solid compounds could be added to the training set, since density and refractive index measurements were reported for the same higher temperature. Even the highest correction amounted to only 0.0494, which is about 1% of the mean value of M.R.s in the training set.
With the exception of anthracene derivatives, the measurements agreed well with the CMR calculations. The average deviation for four anthracene analogs is 0.386 after the temperature corrections were made. Since one phenanthrene and a dozen naphthalene analogs are predicted well, it seems that anthracene analogs must remain anomalous for the present.
4. Bibliography
- A.I. Vogel, J. Chem. Soc., (1948) 1833.>
- A.I. Vogel, W.T. Cresswell, G. J. Jeffery, & J. Leicester, Chem. & Indust., (1950), 358.>
- S. Glasstone, "Textbook of Physical CHemistry" 2nd Ed., D. VanNostrand, N.Y., (1946), p. 529.>
- C.Hansch, A. Leo, S. Unger, K.H. Kim, D. Nikaitani, & E. Lien, J. Med. Chem.,16, 1207 (1973).>
- A. Carotti, R.N. Smith, S. Wong, C. Hansch, J. Blaney & R. Langridge, Arch. Biochem. Biophys.,229,112(1984).>
- J. Schuyler, L. Blom & D. van Krevelen, Farad. Soc., 49, 1391 (1953).>
- G.H. Jeffery, R. Parker, & A. I. Vogel, J. Chem. Soc., (1961) 570, and references cited therein.>
- International Critical tables, E. Washburn, Ed., McGraw-Hill, N.Y., (1926), Vol. 1.>
- Beilstein's Handbuch der Organische Chemie, I-IV Erganzungwerke, Springer Verlag, Berlin, (1976).>
- Aldrich Catalog/Handbook of Fine Chemicals, (1984-5), Milwaukee.>
- Eisenlohr, Z. Phys. Chem., 79, 129(1912).>
- K. G. Denbigh, Trans. Farad. Soc., 36, 936 (1940).>
- S. Batsonov, "Refractometry & Chemical Structure", Consultants Bureau, N.Y., (1961).>
- K. Miller and J. Savchik, J. Am. Chem. Soc., 101, 7206 (1979).>
- C. Cumper, A. I. Vogel & S. Walker, J. Chem. Soc., (1956) 3621; ibid.,(1959)3521.>
5. Appendix - Examples

SMILES: COC(=N)c1ccccn1 |
Hydrogens 8 * 0.0887 = 0.7096 Atom value for C 2 * 0.2864 = 0.5728 Atom value for N 1 * 0.2800 = 0.2800 Atom value for O 1 * 0.1531 = 0.1531 Atom value for c 5 * 0.2864 = 1.4320 Atom value for n 1 * 0.1640 = 0.1640 Bond value for aromatic bonds 6 * 0.0730 = 0.4380 |
High confidence CMR estimate 3.7495 |

SMILES: N#Cc1ccco1 |
Hydrogens 3 * 0.0887 = 0.2661 Atom value for C 1 * 0.2864 = 0.2864 Atom value for N 1 * 0.2800 = 0.2800 Atom value for c 4 * 0.2864 = 1.1456 Atom value for o 1 * 0.0371 = 0.0371 Bond value for aromatic bonds 5 * 0.0730 = 0.3650 |
High confidence CMR estimate 2.3802 |
SMILES: CN(C)[As]1OCCO1 |
Hydrogens 10 * 0.0887 = 0.8870 Atom value for C 4 * 0.2864 = 1.1456 Atom value for N 1 * 0.2800 = 0.2800 Atom value for O 2 * 0.1531 = 0.3062 Atom value for As 1 * 1.1750 = 1.1750 Bond value for As-O 2 * -.0625 = -0.1250 |
High confidence CMR estimate 3.6688 |
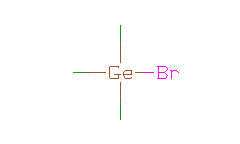
SMILES: C[Ge](C)(C)Br |
Hydrogens 9 * 0.0887 = 0.7983 Atom value for C 3 * 0.2864 = 0.8592 Atom value for Ge 1 * 0.9536 = 0.9536 Atom value for Br 1 * 0.8657 = 0.8657 |
High confidence CMR estimate 3.4768 |

SMILES: BrC(=COCC#C)Br |
Hydrogens 4 * 0.0887 = 0.3548 Atom value for C 5 * 0.2864 = 1.4320 Atom value for O 1 * 0.1531 = 0.1531 Atom value for Br 2 * 0.8657 = 1.7314 Chain C=C unsaturation 0.1520 Terminal C#C unsaturation 0.1520 |
High confidence CMR estimate 3.9753 |
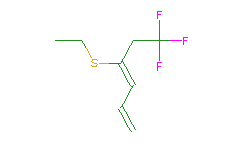
SMILES: CCSC(=CC=C)CC(F)(F)F |
Hydrogens 11 * 0.0887 = 0.9757 Atom value for C 8 * 0.2864 = 2.2912 Atom value for F 3 * 0.1042 = 0.3126 Atom value for S 1 * 0.8063 = 0.8063 Chain C=C(-) conjugation 0.2280 Chain C=C(-) conjugation 0.2280 |
High confidence CMR estimate 4.8418 |

SMILES: CCN1CC(C(C)C=N1)C(=O)C |
Hydrogens 16 * 0.0887 = 1.4192 Atom value for C 9 * 0.2864 = 2.5776 Atom value for N 2 * 0.2800 = 0.5600 Atom value for O 1 * 0.1531 = 0.1531 Bond value for C=O 1 * 0.0600 = 0.0600 (*)C=N(*) UNSATURATION 0.1520 |
High confidence CMR estimate 4.9219 |

SMILES: O=COCC(COC=O)OC=O |
Hydrogens 8 * 0.0887 = 0.7096 Atom value for C 6 * 0.2864 = 1.7184 Atom value for O 6 * 0.1531 = 0.9186 Bond value for C=O 3 * 0.0600 = 0.1800 |
High confidence CMR estimate 3.5266 |
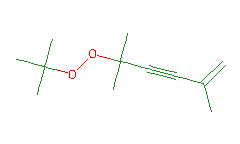
SMILES: CC(=C)C#CC(C)(C)OOC(C)(C)C |
Hydrogens 20 * 0.0887 = 1.7740 Atom value for C 12 * 0.2864 = 3.4368 Atom value for O 2 * 0.1531 = 0.3062 Bond value for O-O 1 * 0.1270 = 0.1270 Chain C=C(-) conjugation 0.2280 Interior C#C(-) conjugation 0.2280 |
High confidence CMR estimate 6.1000 |
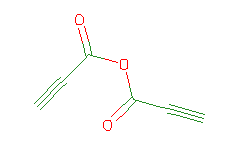
SMILES: O=C(OC(=O)C#C)C#C |
Hydrogens 2 * 0.0887 = 0.1774 Atom value for C 6 * 0.2864 = 1.7184 Atom value for O 3 * 0.1531 = 0.4593 Bond value for C=O 2 * 0.0600 = 0.1200 Terminal C#C(+) conjugation 0.2280 Terminal C#C(+) conjugation 0.2280 |
High confidence CMR estimate 2.9311 |

SMILES: CC(=O)C#Cc1ccccc1 |
Hydrogens 8 * 0.0887 = 0.7096 Atom value for C 4 * 0.2864 = 1.1456 Atom value for O 1 * 0.1531 = 0.1531 Atom value for c 6 * 0.2864 = 1.7184 Bond value for aromatic bonds 6 * 0.0730 = 0.4380 Bond value for C=O 1 * 0.0600 = 0.0600 Interior (-)C#C(+) conjugation 0.4560 |
High confidence CMR estimate 4.6807 |
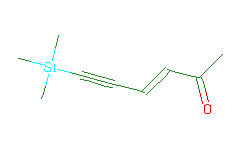
SMILES: CC(=O)C=CC#C[Si](C)(C)C |
Hydrogens 14 * 0.0887 = 1.2418 Atom value for C 9 * 0.2864 = 2.5776 Atom value for O 1 * 0.1531 = 0.1531 Atom value for Si 1 * 0.7087 = 0.7087 Bond value for C=O 1 * 0.0600 = 0.0600 Chain (-)C=C(+) conjugation 0.4560 Interior C#C(-) conjugation 0.2280 |
High confidence CMR estimate 5.4252 |

SMILES: CCCNN=Cc1ccccc1 |
Hydrogens 14 * 0.0887 = 1.2418 Atom value for C 4 * 0.2864 = 1.1456 Atom value for N 2 * 0.2800 = 0.5600 Atom value for c 6 * 0.2864 = 1.7184 Bond value for aromatic bonds 6 * 0.0730 = 0.4380 (-)C=N(*) CONJUGATION 0.3040 |
High confidence CMR estimate 5.4078 |
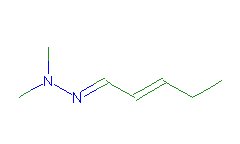
SMILES: CCC=CC=NN(C)C |
Hydrogens 14 * 0.0887 = 1.2418 Atom value for C 7 * 0.2864 = 2.0048 Atom value for N 2 * 0.2800 = 0.5600 Chain C=C(+) conjugation 0.2280 (-)C=N(*) CONJUGATION 0.3040 |
High confidence CMR estimate 4.3386 |
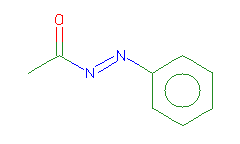
SMILES: CC(=O)N=Nc1ccccc1 |
Hydrogens 8 * 0.0887 = 0.7096 Atom value for C 2 * 0.2864 = 0.5728 Atom value for N 2 * 0.2800 = 0.5600 Atom value for O 1 * 0.1531 = 0.1531 Atom value for c 6 * 0.2864 = 1.7184 Bond value for aromatic bonds 6 * 0.0730 = 0.4380 Bond value for C=O 1 * 0.0600 = 0.0600 Chain (-)N=N(+) conjugation missing |
CMR uncertain due to missing CONJUGATION 4.2119 |

SMILES: CC[Zn]CC |
Hydrogens 10 * 0.0887 = 0.8870 Atom value for C 4 * 0.2864 = 1.1456 Atom value for Zn missing |
INVALID CMR due to missing ATOM value 2.0326 |

SMILES: BrN1C(=O)CCC1=O |
Hydrogens 4 * 0.0887 = 0.3548 Atom value for C 4 * 0.2864 = 1.1456 Atom value for N 1 * 0.2800 = 0.2800 Atom value for O 2 * 0.1531 = 0.3062 Atom value for Br 1 * 0.8657 = 0.8657 Bond value for Br-N missing Bond value for C=O 2 * 0.0600 = 0.1200 |
CMR uncertain due to missing BOND value 3.0723 |